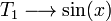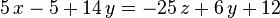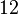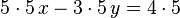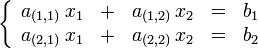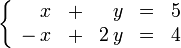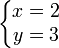Un sistema lineal de dos ecuaciones con dos incógnitas es un sistema lineal de ecuaciones formado por sólo dos ecuaciones que admite un tratamiento particularmente simple, junto con el caso trivial de una ecuación lineal con una única incógnita, es el caso más sencillo posible de sistemas de ecuaciones, y que permiten su resolución empleando técnicas básicas del álgebra cuando los coeficientes de la ecuación se encuentran sobre un cuerpo (sobre un anillo la solución no es tan sencilla).
Una infinidad de problemas pueden ser resueltos con un sistema de dos ecuaciones. Veamos las distintas formas en las que se pueden encontrar sus soluciones.
Antes de afrontar las formas de resolver un sistema de ecuaciones
vamos a ver algunos términos y conceptos, que si bien son comunes a
todas las ecuaciones y sistemas de ecuaciones, conviene recordarlos
antes.
En cada uno de los miembros hay uno o más términos. Un término es una parte de la expresión relacionada término de una ecuación puede ser un monomio o una expresión transcendente.
Dada la ecuación:
Para finalizar esta sección podemos decir que si una ecuación se multiplica por un escalar, la ecuación no varia, así la ecuación:
En una ecuación
Una ecuación es una expresión matemática en la que hay dos partes equivalentes, separadas con un signo igual (=). Cada una de estas partes es un miembro de la ecuación; naturalmente una ecuación está formada por dos miembros separados por el signo igual.En cada uno de los miembros hay uno o más términos. Un término es una parte de la expresión relacionada término de una ecuación puede ser un monomio o una expresión transcendente.
Dada la ecuación:
- Si en uno de los términos hay una función trascendente, la ecuación es trascendente.
- Si no es transcendente, el grado de la ecuación es el grado del término de mayor grado.
Ecuación lineal
En una ecuación lineal cada término está formado por un coeficiente y una incógnita, no elevada a ninguna potencia (con potencia 1, pero no se pone), y términos que no tienen incógnita. Los términos con incógnita se llaman término en..., esa incógnita; los términos que no tienen incógnita se llaman términos independientes. En la ecuación:Para finalizar esta sección podemos decir que si una ecuación se multiplica por un escalar, la ecuación no varia, así la ecuación: