Número complejo
Se puede considerar C como el conjunto de los pares ordenados de números reales z=(x,y) con las siguientes operaciones:| Elemento
neutro: | |
| Elemento
opuesto: | |
| Elemento
unidad: | |
Elemento
inverso: 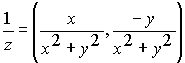 , siempre que , siempre que |
| El cuerpo de los complejos es lo que se denomina
un cuerpo algebraicamente cerrado,
es decir, toda ecuación algebraica (polinómica) con coeficientes complejos
tiene siempre al menos una raíz compleja (y por tanto las tiene todas). | |
| El cuerpo de los complejos no es un cuerpo ordenado. No puede darse en C una relación de orden total que respete las operaciones de suma y producto. No tiene por tanto sentido comparar dos números complejos en la manera en que estamos acostumbrados a hacer con los reales. |
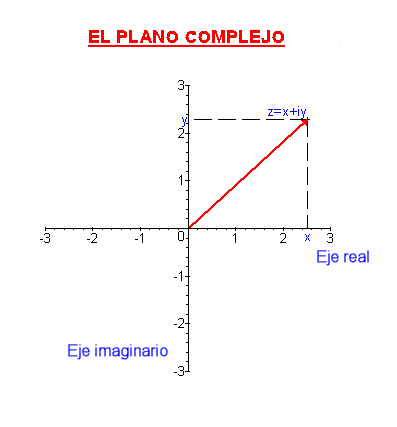
Obviamente, dos números complejos son iguales si y sólo si lo son simultáneamente sus partes reales y sus partes imaginarias.
Usando este tipo de representación, la suma de complejos se corresponde con la suma de vectores. Dados dos vectores
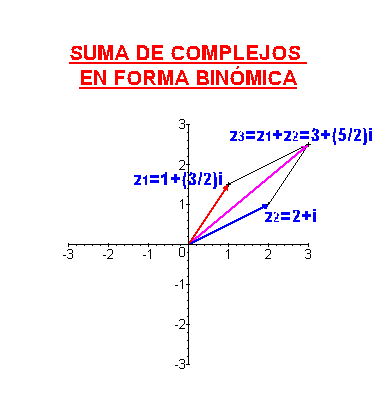
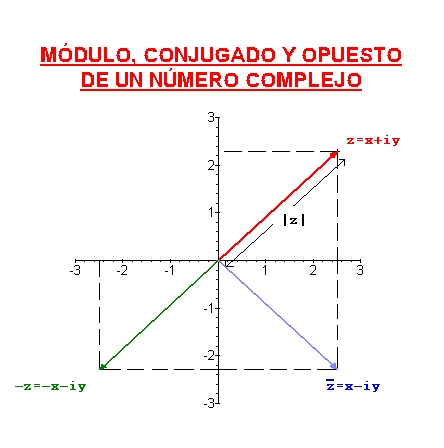
Se define el módulo de un número complejo como el módulo del vector que lo representa, es decir, si
El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si
El opuesto de un número complejo es su simétrico respecto del origen.
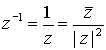 .
.En vez de usar coordenadas cartesianas para representar a los puntos del plano podemos usar coordenadas polares, lo que da lugar a la siguiente forma de representación de los números complejos.
2. Forma polar o
módulo-argumento
Otra forma de expresar un número complejo es la forma polar o
forma módulo-argumento,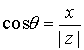 ,
, 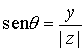 .
.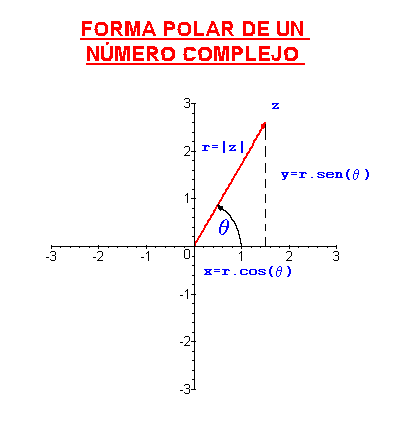
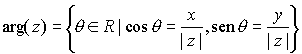
Se verifica entonces que
La forma polar de un número complejo es especialmente cómoda a la hora de multiplicar, ya que basta con multiplicar los módulos y sumar los argumentos, es decir, si
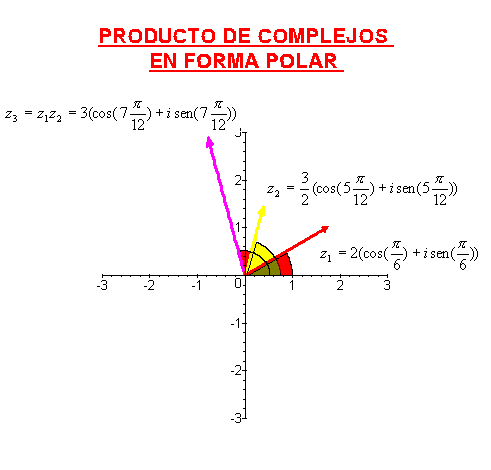
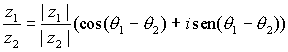 ,
,Las fórmulas anteriores pueden generalizarse para el producto de varios complejos, así, si
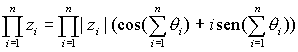
En particular tenemos otra expresión para el inverso de un número no nulo,
(Aquí puedes ver una aplicación de la fórmula de Moivre)
Cambio de binómica a
polar
|
Cambio de polar a
binómica
|
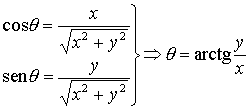 |
Una variante de la forma polar se obtiene al tener en cuenta la conocida como fórmula de Euler:
Esto nos permite escribir un número complejo en la forma siguiente, denominada forma exponencial:
Esto nos permite dar una nueva expresión para el inverso de un complejo no nulo en la forma
Estudiemos ahora las potencias con exponente racional de un número complejo. Dado
Si
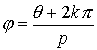 , para
, para De todos estos valores sólo p consecutivos son distintos, el resto resulta ser repetición sucesiva de valores ya obtenidos. Por tanto, un número complejo tiene siempre p raíces p-ésimas distintas
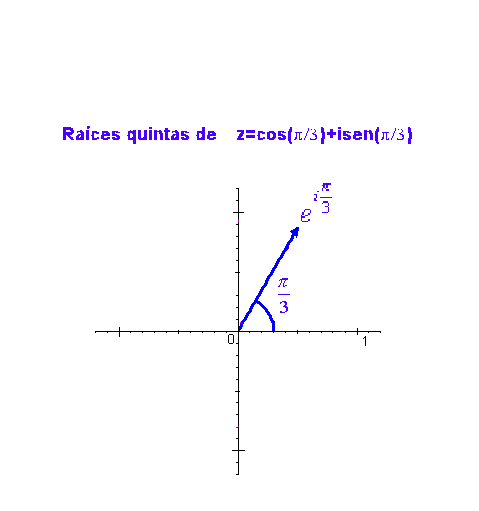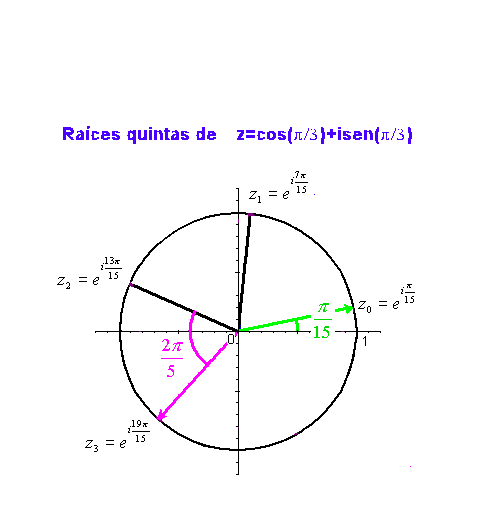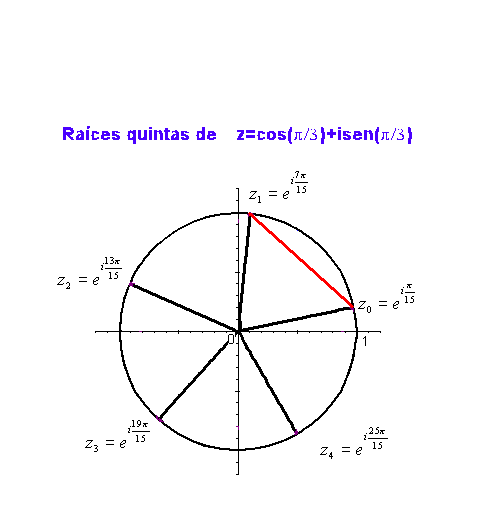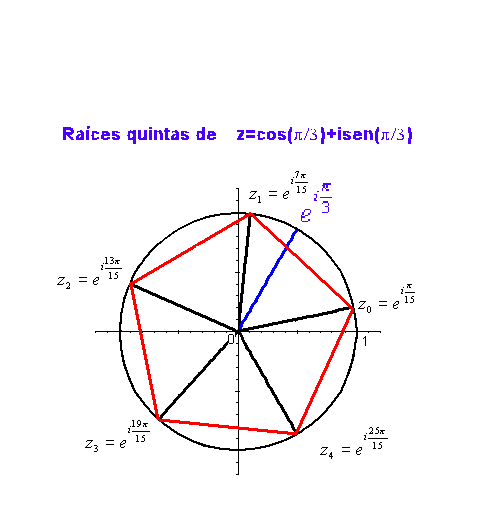
Como ejemplo, en la siguiente gráfica podemos ver las raíces quintas de

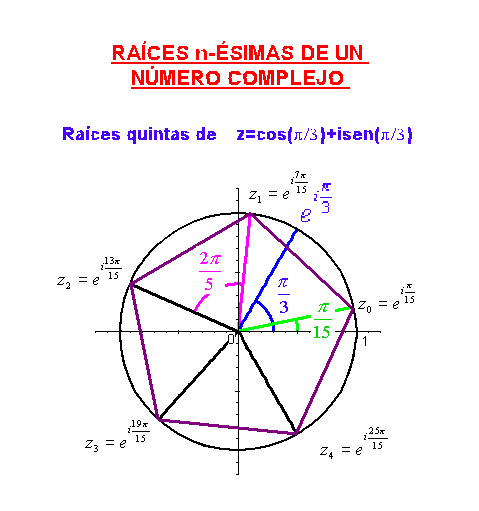
Puede verse lo mismo en la siguiente animación: