Número complejo
Se puede considerar C como el conjunto de los pares ordenados de números reales z=(x,y)
con las siguientes
operaciones:
Con estas operaciones C tiene la estructura de
cuerpo
conmutativo
 |
Elemento
neutro:  |
 |
Elemento
opuesto: 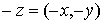 |
 |
Elemento
unidad: 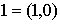 |
 |
Elemento
inverso: 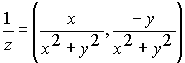 , siempre que , siempre que 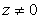

|
Nótese que el complejo (0,1) verifica
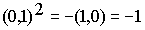
, es decir,
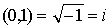
(link
a explicación de extensión de R añadiendo raices de ecuaciones algebraicas
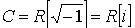
)
 |
El cuerpo de los complejos es lo que se denomina
un cuerpo algebraicamente cerrado,
es decir, toda ecuación algebraica (polinómica) con coeficientes complejos
tiene siempre al menos una raíz compleja (y por tanto las tiene todas).

|
 |
El cuerpo de los complejos
no es un cuerpo ordenado. No
puede darse en C una relación de orden total que respete las operaciones
de suma y producto. No tiene por tanto sentido comparar dos números
complejos en la manera en que estamos acostumbrados a hacer con los
reales. |
Podemos considerar C como un
espacio vectorial
isomorfo a
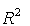
, de este modo se tiene:
Gráficamente, podemos representar
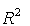
(y por tanto C)
como un plano.
Para cada número complejo z, la primera componente,
x,
se denomina
parte real y la segunda,
y, se denomina
parte
imaginaria.
Obviamente, dos números complejos son iguales si y sólo si lo
son simultáneamente sus partes reales y sus partes imaginarias.
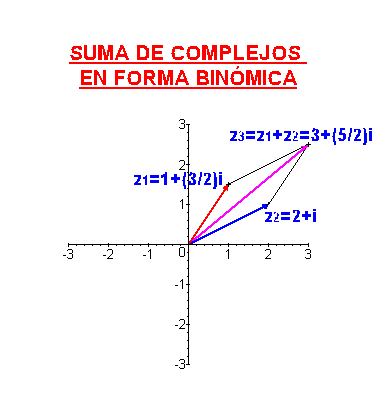
Usando este tipo de representación, la
suma de complejos se corresponde con la suma de vectores.
Dados dos vectores
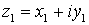
y
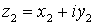
su suma es
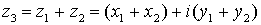
Se define el
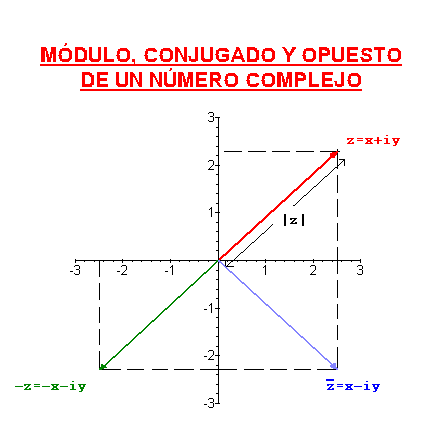
módulo de un número complejo como el
módulo del vector que lo representa, es decir, si
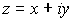
, entonces el
módulo de
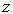
es
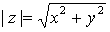
.
El
conjugado de un número complejo se
define como su simétrico respecto del eje real, es decir, si
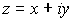
, entonces el
conjugado de
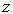
es
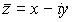
.
El
opuesto de un número complejo es su
simétrico respecto del origen.
Es fácil ver que se cumple,
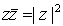
, por tanto
podemos expresar el inverso de un número
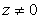
en la forma
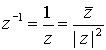
.
En vez de usar coordenadas cartesianas para representar a los
puntos del plano podemos usar coordenadas polares, lo que da lugar a la
siguiente forma de representación de los números complejos.
Otra forma de expresar un número complejo es la forma polar o
forma módulo-argumento,
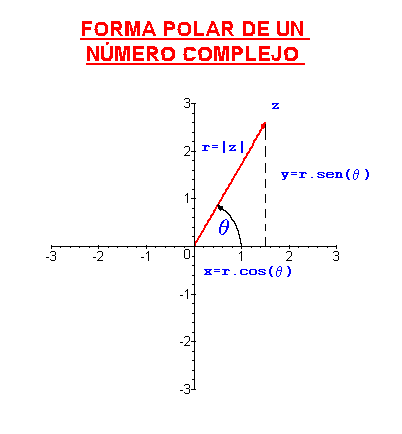
donde
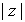
es el módulo de
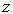
, y donde
q
es un
argumento de
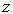
, esto es,
q
es un ángulo tal que
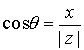
,
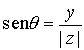
.
NOTA: Un número complejo tiene infinitos argumentos
distintos. De hecho se puede definir el argumento de un número complejo no nulo
como el conjunto de todos los posibles valores
q
que verifican lo anterior, es decir,
Es claro, por tanto, que si
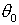
es un valor particular del
argumento de
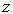
, entonces
Se denomina
argumento principal
al único valor
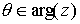
tal que
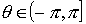
, y se denota
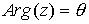
Se verifica entonces que
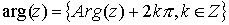
.
Dos números complejos
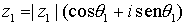
y
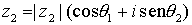
, representados en forma
polar son iguales si y sólo si sus módulos son iguales
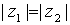
, y sus argumentos se diferencian
en un número entero de vueltas, es decir,
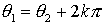
, con
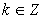
.
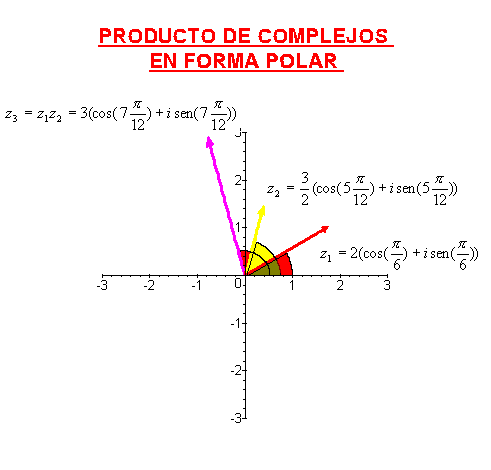
La forma polar de un número
complejo es especialmente cómoda a la hora de multiplicar, ya que basta con
multiplicar los módulos y sumar los argumentos, es decir, si
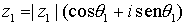
, y
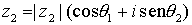
,
entonces
Del mismo modo se puede calcular el cociente de un complejo por
otro no nulo sin más que dividir los módulos y restar los argumentos:
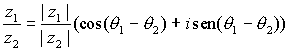
,
siempre que
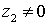
.
Las fórmulas anteriores pueden generalizarse para el producto
de varios complejos, así, si
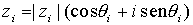
, para
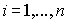
,
entonces
Finalmente, en el caso en que todos los factores sean iguales se
obtiene la
fórmula de Moivre:
Esta fórmula es también válida para exponentes enteros
negativos, siempre que
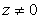
.
En particular tenemos otra expresión para el inverso de un
número no nulo,
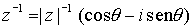
.
(Aquí puedes ver una
aplicación de la fórmula
de Moivre)
Cambio de binómica a
polar
|
Cambio de polar a
binómica
|
|
|
|
3. Forma exponencial
Una variante de la forma polar se obtiene al tener en cuenta
la conocida como
fórmula de Euler:
para
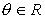
.
Esto nos permite escribir un número complejo en la forma
siguiente, denominada forma exponencial:
Esta nueva forma es especialmente cómoda para expresar
productos y cocientes ya que sólo hay que tener en cuenta las propiedades de la
función exponencial (para multiplicar se suman exponentes y para dividir se
restan). En particular, para potencias con exponentes enteros se tiene
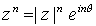
.
Esto nos permite dar una nueva expresión para el inverso de un
complejo no nulo en la forma
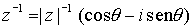
.
Estudiemos ahora las potencias con exponente racional de un
número complejo. Dado
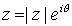
, sea
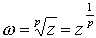
, para un número natural p.
Si
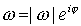
, puesto que
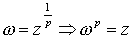
, es decir,
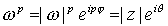
. Por
tanto,
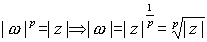
, y además,
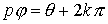
, o sea,
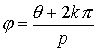
, para
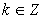
.
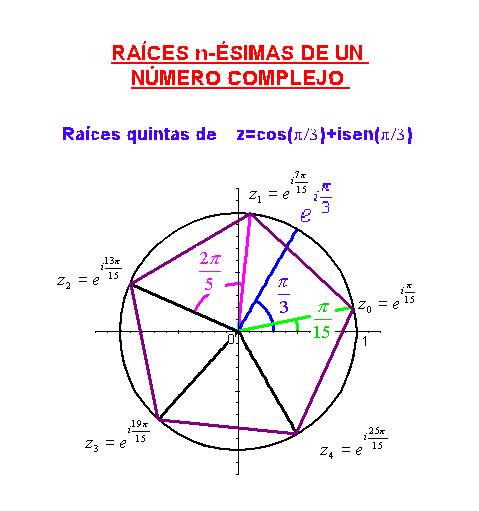
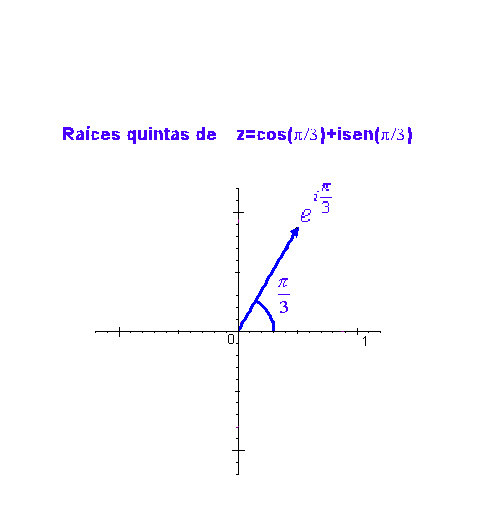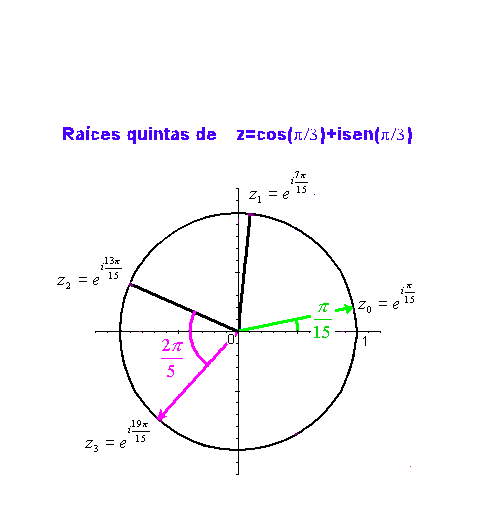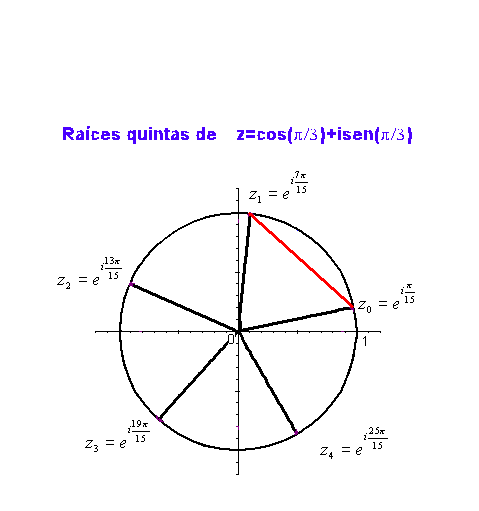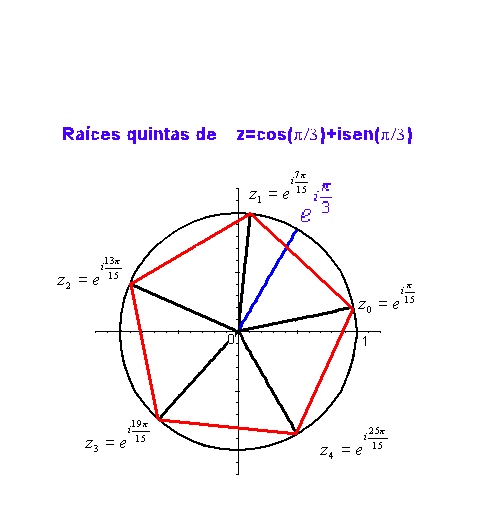
De todos estos valores sólo p consecutivos son distintos, el
resto resulta ser repetición sucesiva de valores ya obtenidos. Por tanto, un
número complejo tiene siempre p raíces p-ésimas distintas
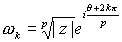
, para
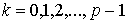
.
Se puede observar que las p raíces pésimas tienen todas el
mismo módulo, y sus argumentos se diferencian en
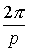
cada uno del
siguiente, esto es, las raíces p-ésimas se encuentran en los vértices de un
polígono regular de p lados incrito en la circunferencia de centro 0 y radio
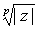
.
Como ejemplo, en la siguiente gráfica podemos ver las raíces
quintas de

Puede verse lo mismo en la siguiente animación:







 , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.




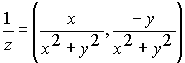 , siempre que
, siempre que 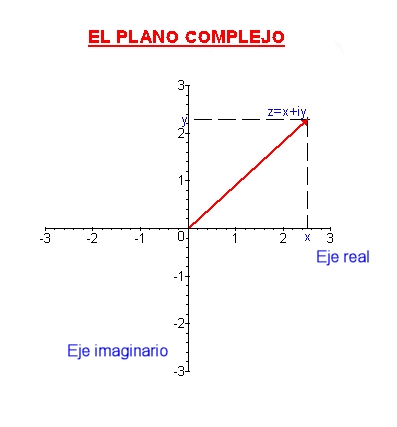
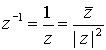 .
.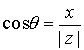 ,
, 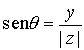 .
.
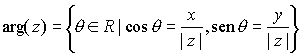
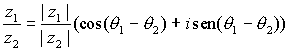 ,
,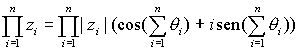
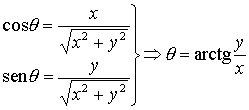
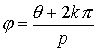 , para
, para